斐波那契数列C语言多种实现方法

math

C语言

2023-02-22 13:36:42

本文将使用C语言通过递归、动态规划、通项公式等技巧来计算斐波那契数列；并获得斐波那契数列的第n项值；

斐波那契数列

斐波那契数列指的是这样一个数列：

0，1，1，2，3，5，8，13，21，34，55，89，144，........

从第3项开始，每一项都等于前两项的和；递推方式定义：

F_n = F_n-1 + F_n-2

且：

F₀ = 0
F₁ = 1

C语言递归实现

#include <stdio.h>

//返回斐波那契数列的第n项
//n从0开始
int fibonacci(int n){
    if (n <= 1){
        return n;
    }
    return fibonacci(n - 1) + fibonacci(n - 2);
}
  
int main(){
    for(int n=0;n<10;n++){
        printf("%d ", fibonacci(n));
    }
    return 0;
}

斐波那契数列前10项：

0 1 1 2 3 5 8 13 21 34

C语言动态规划实现

#include <stdio.h>
int fibonacci(int n){
    int a = 0, b = 1, c, i;
    if (n == 0){
        //第一项为0
        return 0;
    }
    for (i = 2; i <= n; i++) {
        c = a + b; //第n项等于前两项的和
        //更新前两项的值
        a = b;
        b = c;
    }
    return b;
}
int main()
{
	int n = 11;
    printf("%d",fibonacci(n));
	return 0;
}

程序输出：

C语言通项公式实现

斐波那契数列的通项公式为：

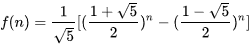
#include <stdio.h>
#include <math.h>

//使用通项公式
int fibonacci(int n){
	return (1/sqrt(5))*(pow((1+sqrt(5))/2,n)-pow((1-sqrt(5))/2,n));
}

int main(){
    for(int n=0;n<10;n++){
        printf("%d ",fibonacci(n));
    }
	return 0;
}

输出：

0 1 1 2 3 5 8 13 21 34

总结

这三种方法中，使用通项公式计算斐波那契数列的性能是好的。