Python计算n阶行列式的值

本文将使用Python编写程序计算n阶行列式的值，不借助第三方库；

n阶行列式的定义

一个n阶行列式可以简单定义为：

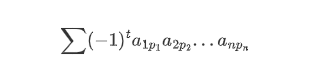
其中 p1 p2 p3 ... pn 为自然数 1，2，...，n 的一个排列；t 为这个排列的逆序数；

计算n阶行列式

程序可计算1~n阶行列式：

def permute(nums):
    #生成n个元素的全排列
    length = len(nums)

    permutations = []

    def _permute(index=0):

        if index == length:
            permutations.append(nums[0:length])
        
        for i in range(index,length):
            nums[i],nums[index] = nums[index],nums[i]
            _permute(index+1)
            nums[i],nums[index] = nums[index],nums[i]
            
    _permute()

    return permutations


def inversion_number(nums):
    #计算排列的逆序数
    count = 0
    for i in range(len(nums)):

        for j in range(i):

            if nums[j] > nums[i]:

                count += 1

    return count

def calculate(det):
    #计算n阶行列式的值

    if not det:#没有元素
        return 0

    if len(det) == 1:#一阶行列式直接返回值
        return det[0]
    
    #生成 1,..., n的全排列
    permutations = permute([i for i in range(1,len(det)+1)])

    result = 0

    for p in permutations:
        #t为逆序数
        t = inversion_number(p)
        product = (-1)**t
        i = 0
        for pn in p:
            product *= det[i][pn-1] #连乘
            i+=1

        result += product #连加

    return result


A = []
A.append([1]) #1阶行列式
A.append(
    [
        [1,2],
        [3,4]
    ]) #2阶行列式

A.append(
    [
        [1,2,3],
        [4,5,6],
        [7,8,9]
    ]) #3阶行列式

for det in A:
    print("Input:")
    for i in det:
        print(i)
    print("value:",calculate(det),"\n")

运行效果

Input:
1
value: 1

Input:
[1, 2]
[3, 4]
value: -2

Input:
[1, 2, 3]
[4, 5, 6]
[7, 8, 9]
value: 0